The Logic of One Point Perspective
Now that we’ve looked at the very basics of perspective, let’s move on to vanishing points. In this section, we’ll build on top of what we discussed here to figure out how vanishing points work and (more importantly) how to use them.
Let’s have a look at a very basic scene. I’ve lined a bunch of sticks , all of the same height, up in a grid.
And this is what it looks like from the side. We’ll examine this side view a bit first.
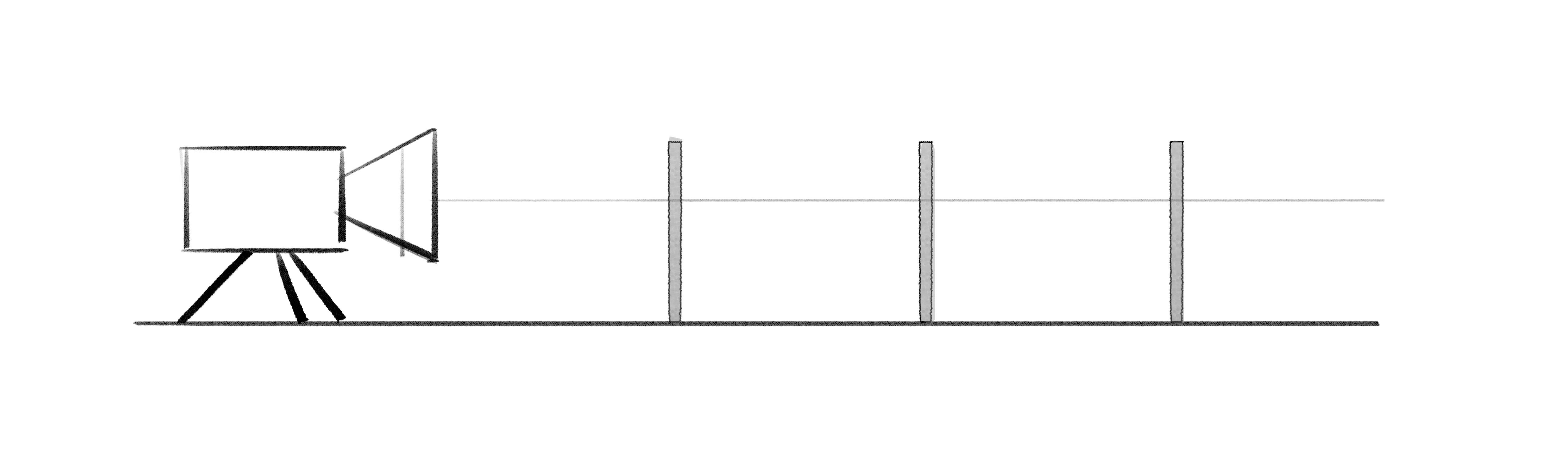
First, let’s shoot some lines of vision out of our camera in side view and see what happens. I’m going to include the horizon line (which, again, is the same as the eye level), as well as lines that hit the tops and bottoms of my sticks.
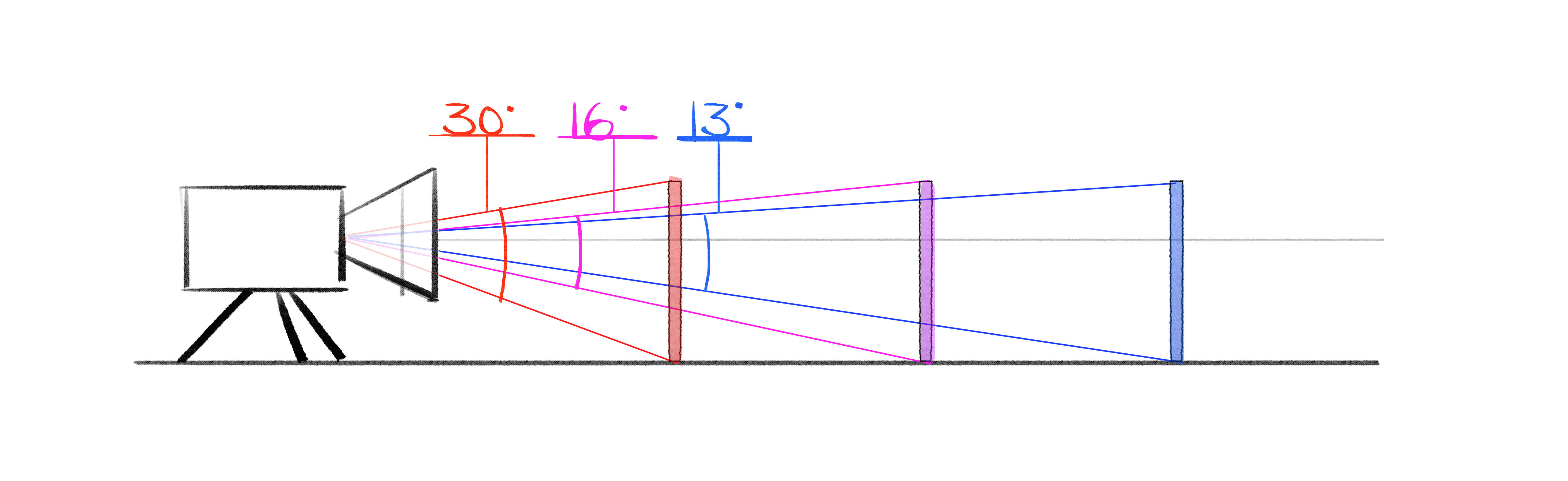
As we can see, the sticks that are farther away from us sit on smaller angles compared to the sticks that are closer to us. However, the horizon line always hits the sticks at about 2/3s of the way up.
If we put a bunch of sticks behind it and zoom way out, we see that eventually, the angle formed by the lines of vision to the top and bottom of the stick get smaller and smaller, until they eventually are nearly the same as the horizon line.
Here we’re going to zoom out a little:
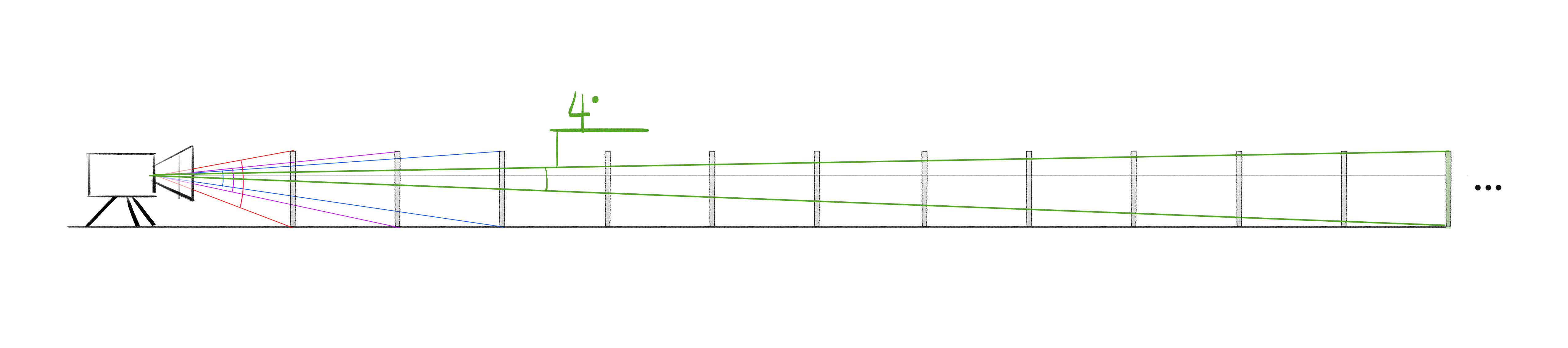
And now we’re gonna zoom way out:

So let’s take stock of what we know so far.
- The farther away things are, the smaller they get (duh),
- The horizon line always runs through the same part of the sticks, no matter how far away they are.
- As our sticks move farther away, they slowly become one with the horizon line.
Let’s shift our focus and look at what this scene looks like from the top. I’ve also shot some lines of vision out from our camera from this angle:
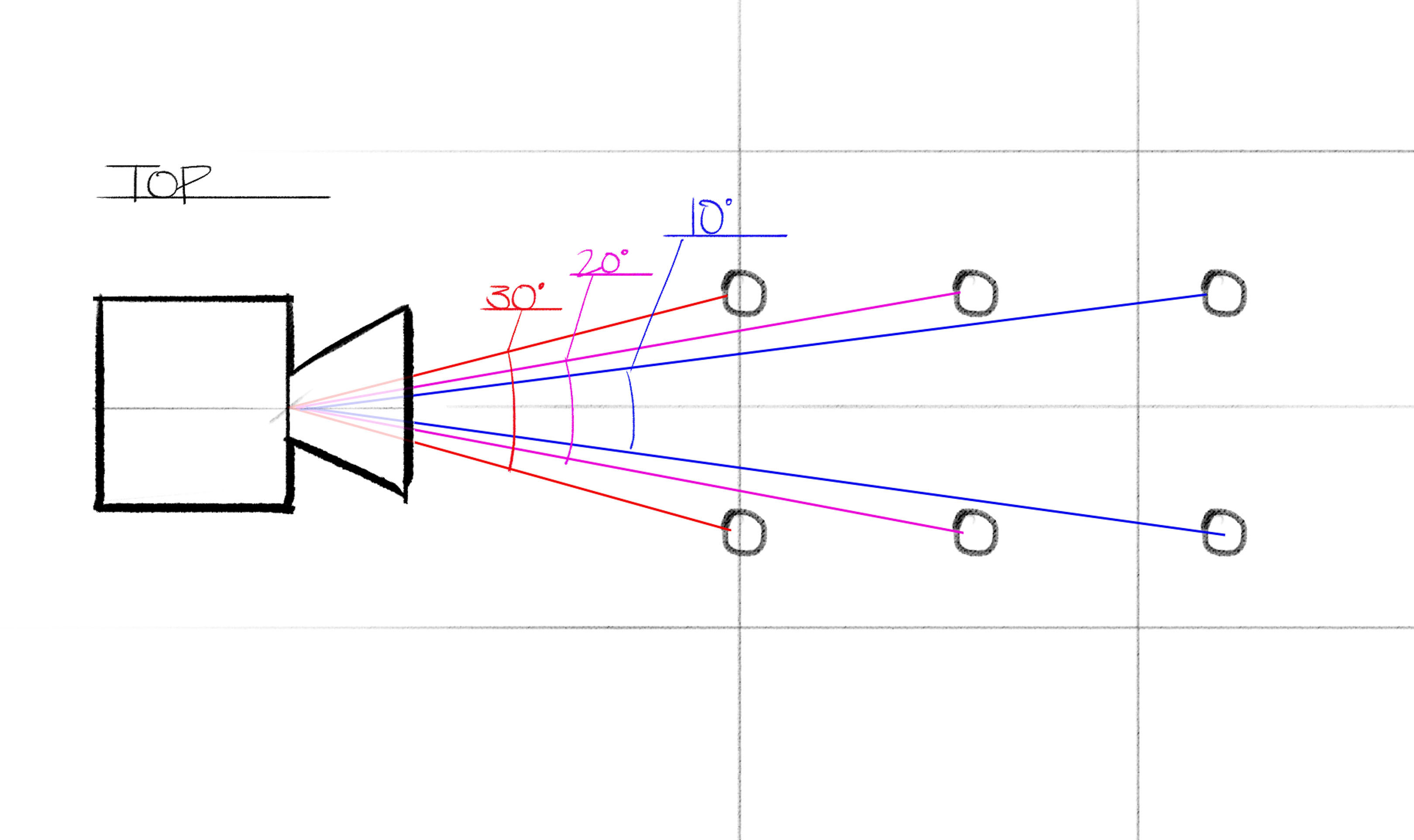
Here’s what it would look like if we put a bunch more sticks behind it and zoomed out:
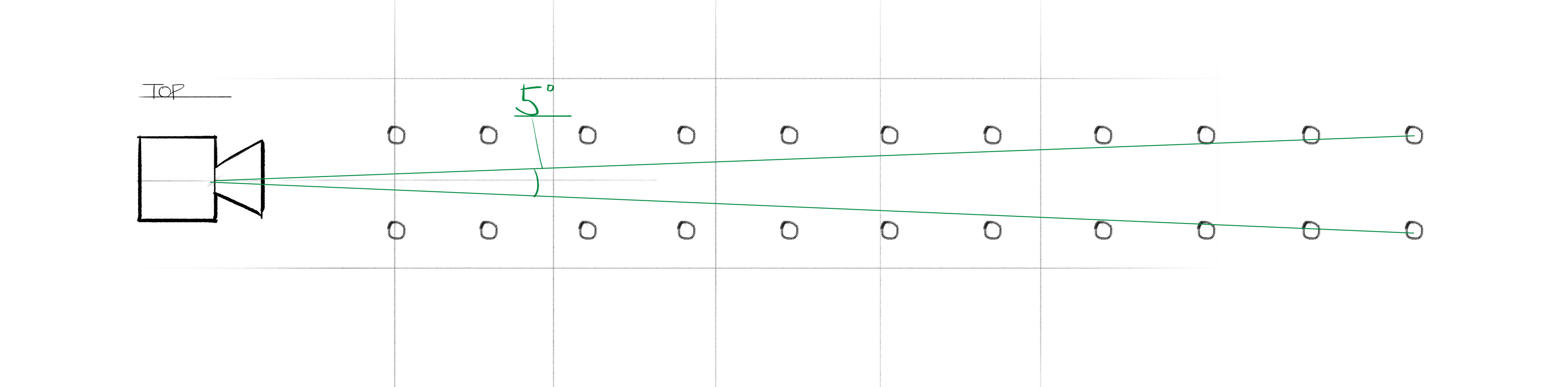
Again, we see that the angles formed by our vision lines get smaller and smaller the farther away the sticks are. Eventually, once the sticks get super far away, those angles are going to get so small that they’re going to be nearly indistinguishable from just one line.
So now let’s try to render this scene out from the point of view from the camera. First, I’m going to set a two things up: what the sticks look like when they’re infinitely far away, and also the closest couple of sticks.
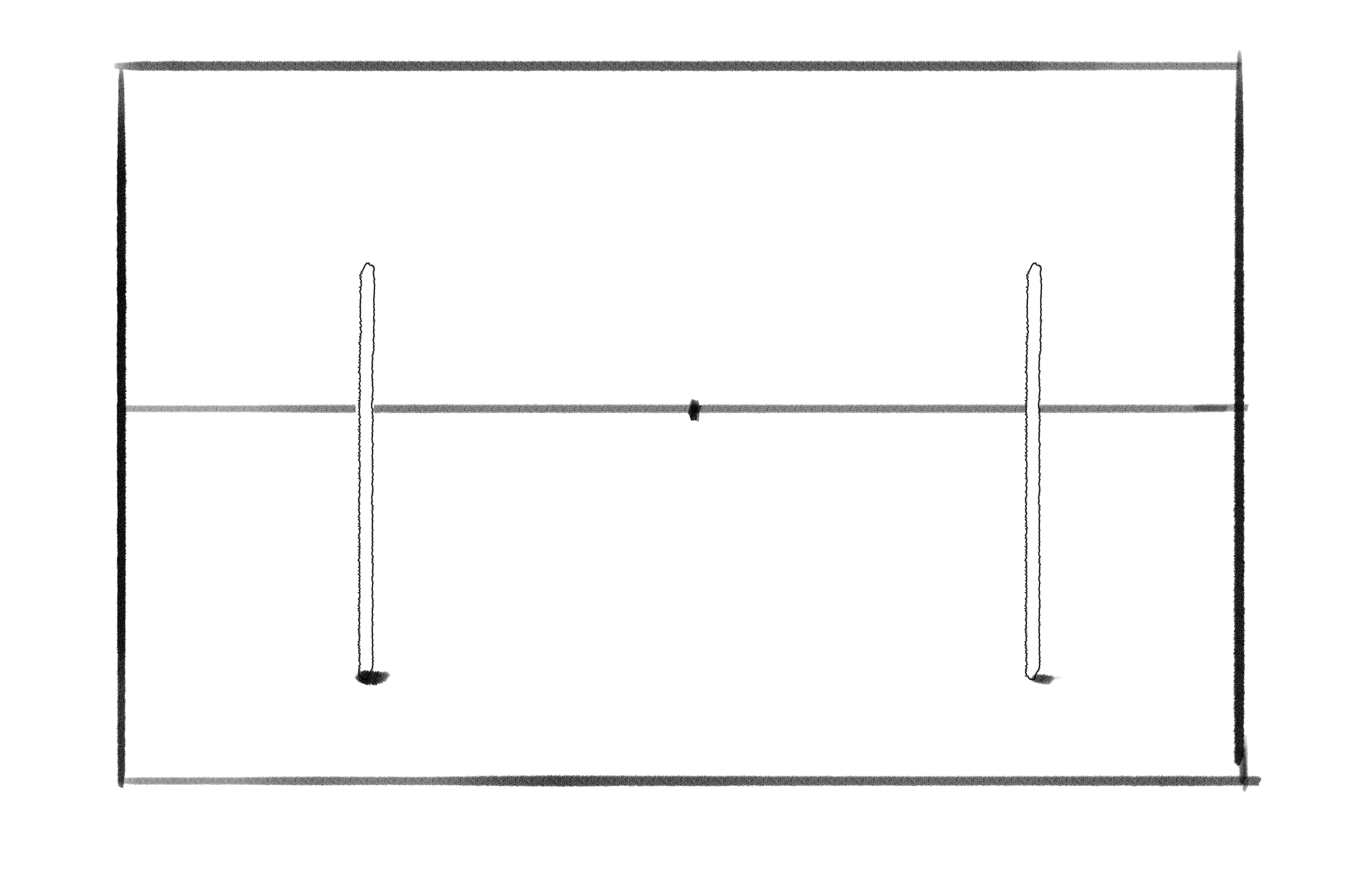
Now, I know that every other pair of sticks behind it is going to be somewhere in between those two sets of sticks. I can draw some lines connecting my two sets of sticks:
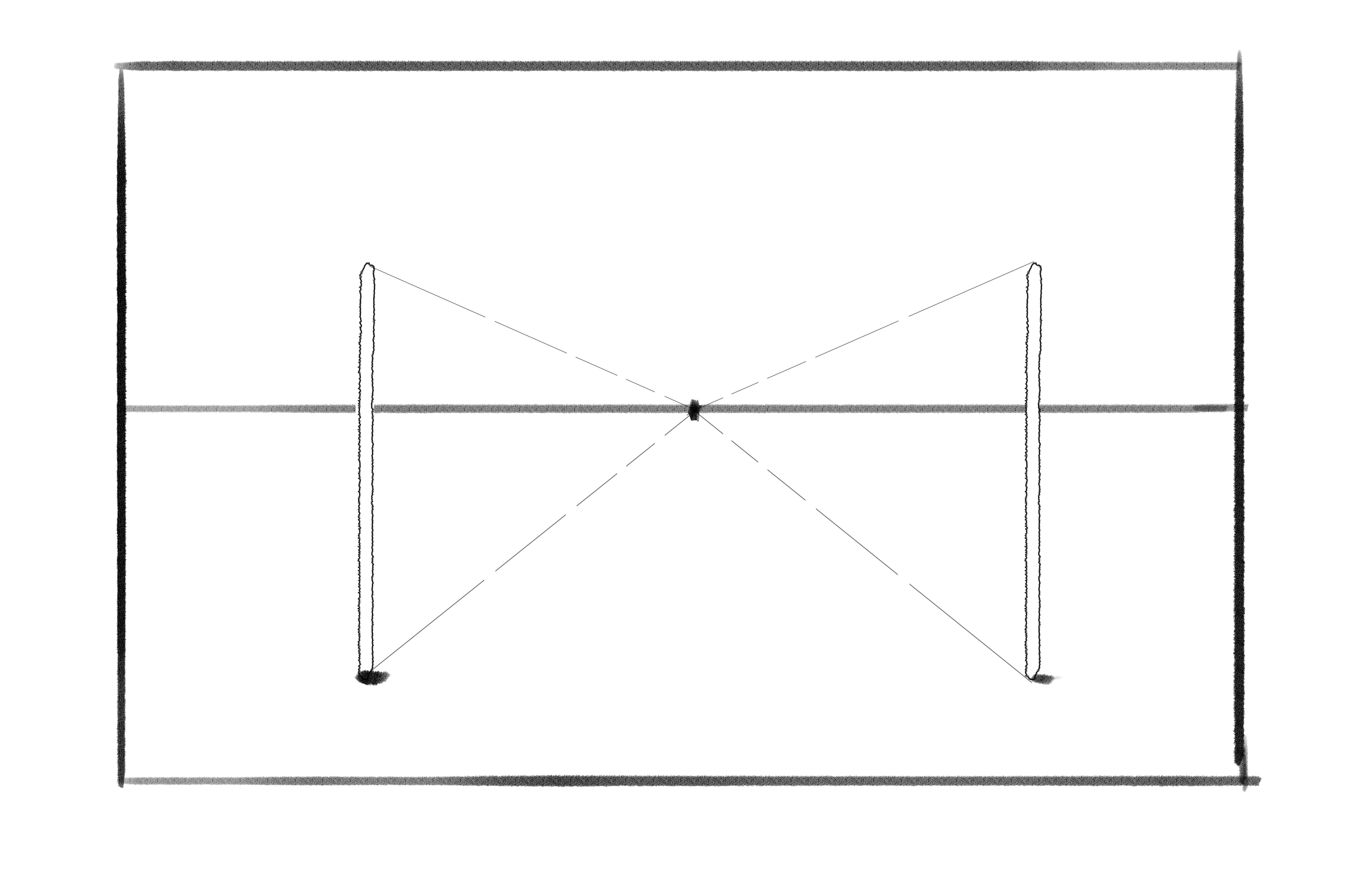
Finally, I’m going to add the extra sets of sticks from my original scene (without all the extra super far-away sticks) by using the guidelines to figure out where they should be:
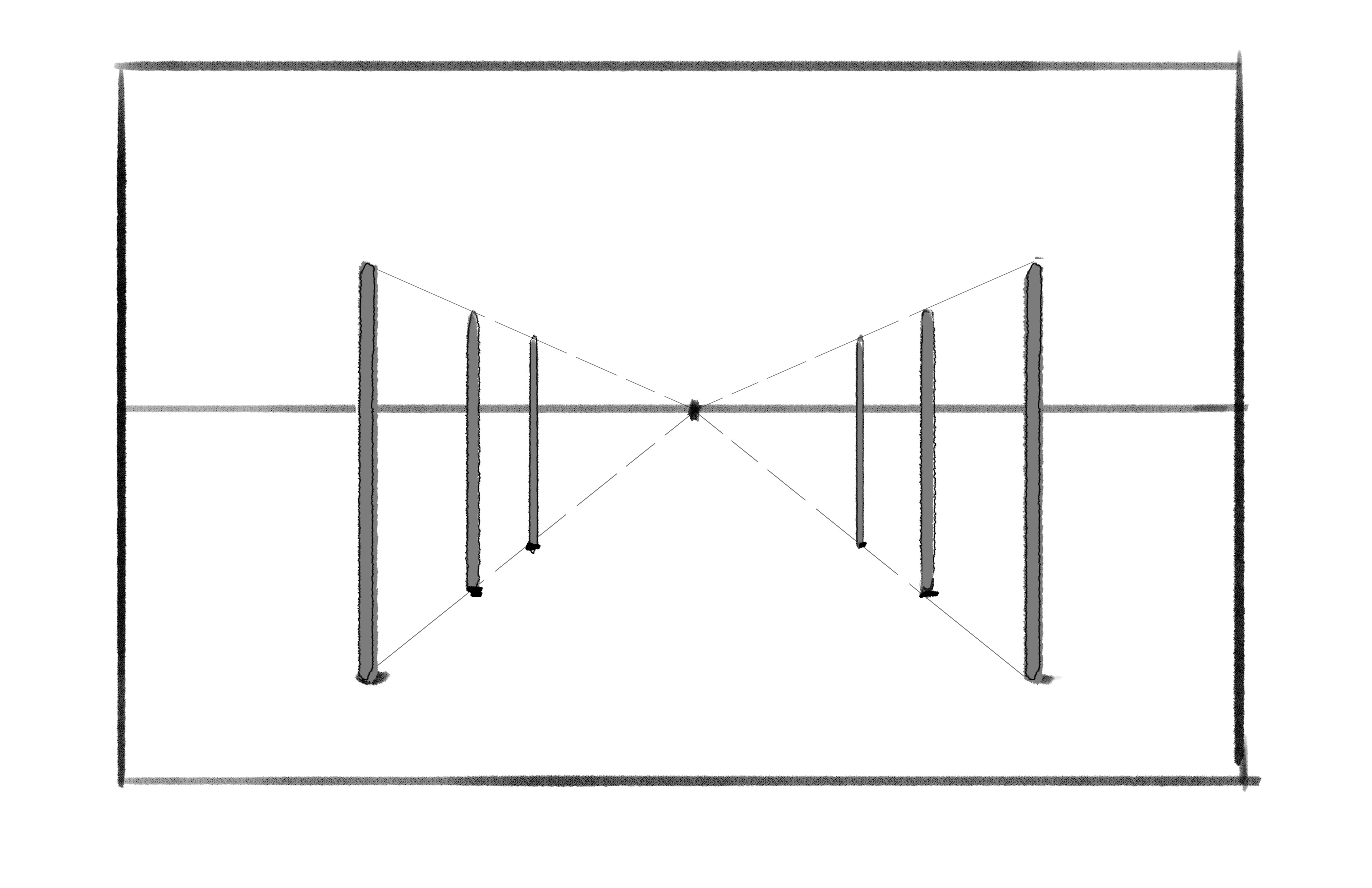
There’s what the camera sees. Notice that if we add in more rows of sticks, and make them go all the way back into the distance, they’ll also eventually get so far away that they’ll be grouped in with the others:
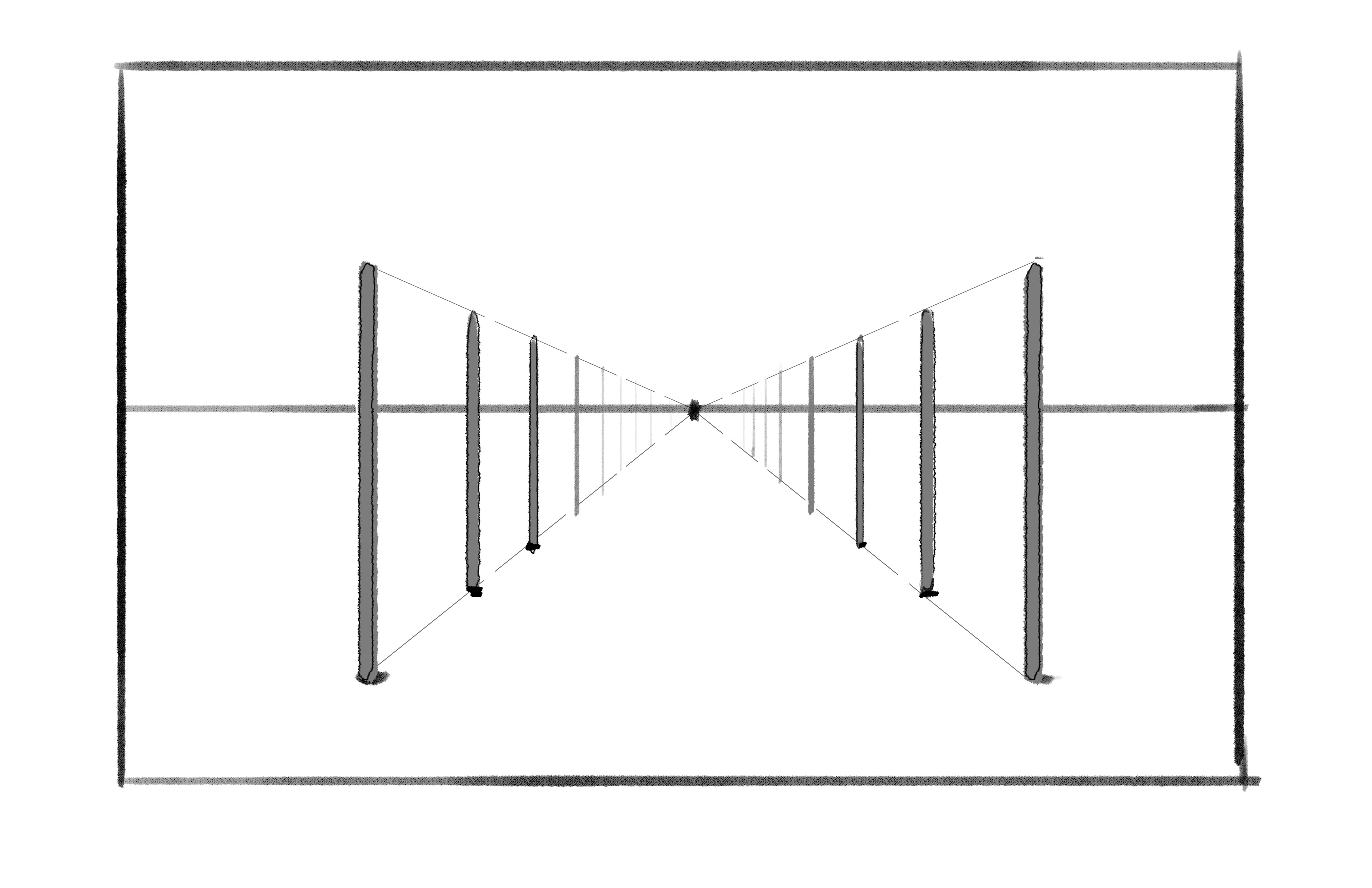
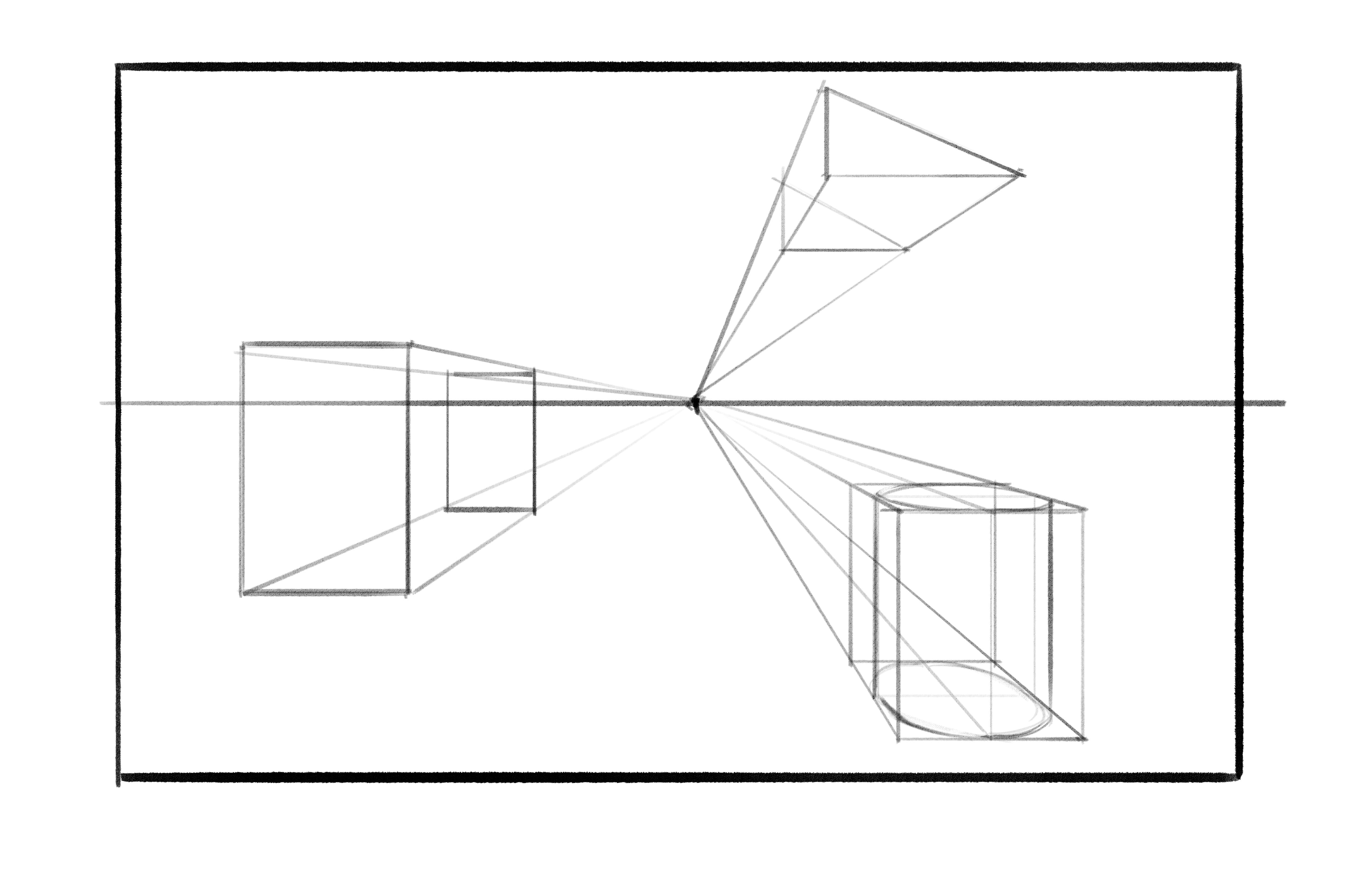
What we’ve just done is set up a one point perspective grid. It’s called that because everything eventually shrinks into one single point on the horizon once they get far away enough. We can use this rule to draw all kinds of things, like cubes, pyramids, and cylinders. Here are a few step-by-steps to figuring out each of these shapes in turn. See if you can apply the logic we just discussed while you stare at these:
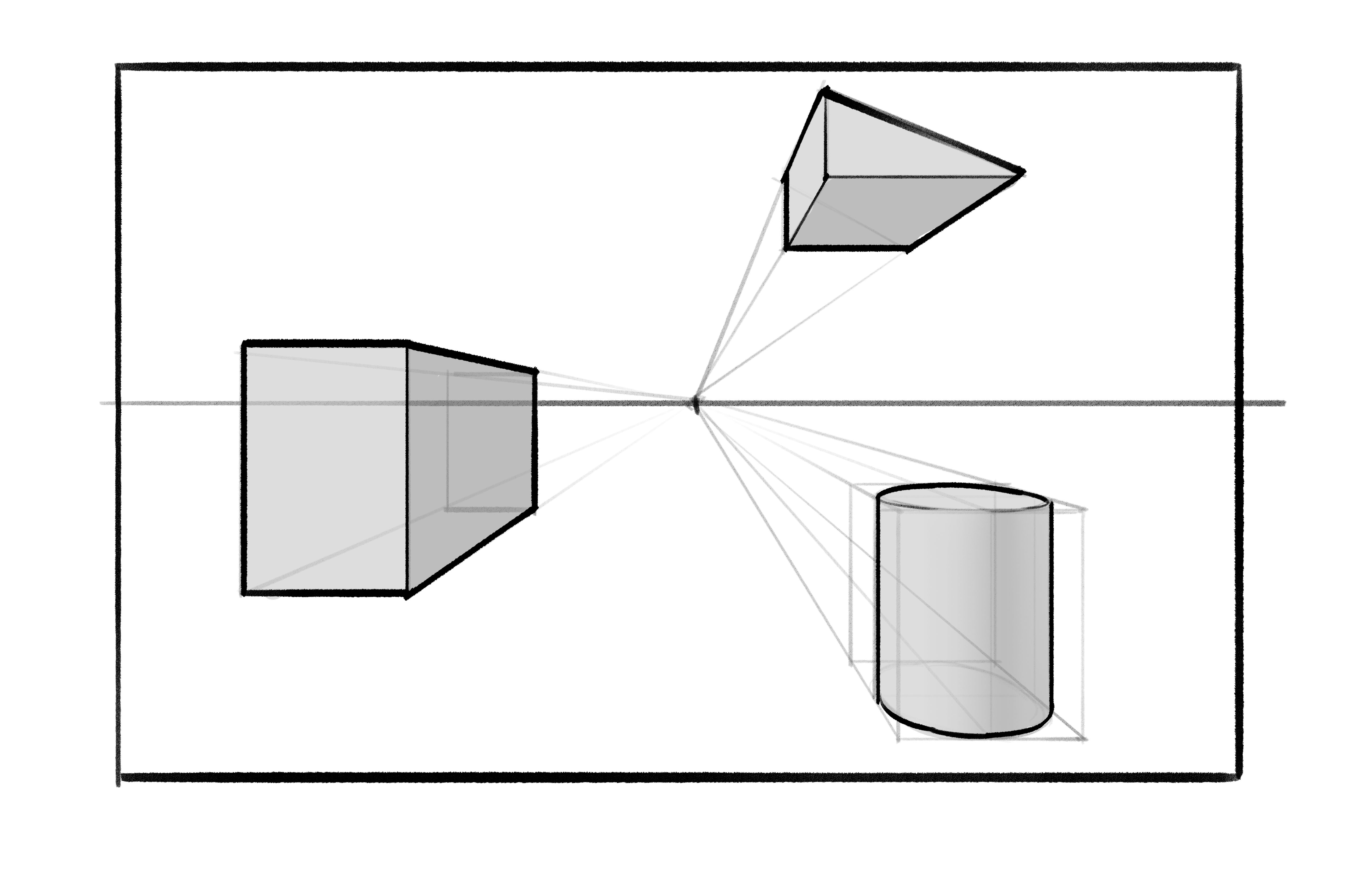
And that’s it! That’s how one point perspective works. This stuff is pretty simple once you lay the steps out one by one, but (brief historical aside incoming) it actually took a while for western civilization to figure out. This flow of logic was originally known to the ancient Greeks and Romans, but was lost at some point after the fall of the Empire. It wasn’t rediscovered until the early to mid-1400s, when an Italian architect re-devised it for his architectural drawings. It’s pretty crazy to think that the world went so long without somebody figuring this out, but I suppose our ancestors were busy with other stuff like not dying from the Plague.
See you next time when we discuss two point perspective!